Решение линейного уравнения теплопроводности (продолжение листинга 11 1)
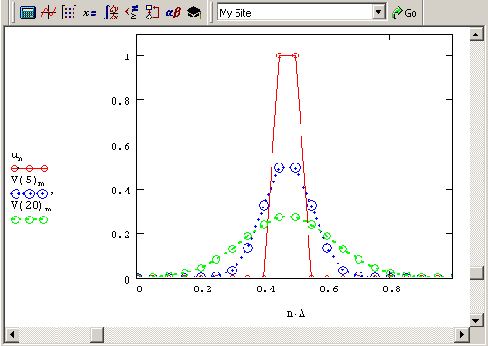
Рисунок 11.7. Решение линейного уравнения теплопроводности (продолжение листинга 11.1)
Примечание 2
Примечание 2
Несколько забегая вперед, заметим, что показанное на Рисунок 11.7 решение и соответствует коэффициенту Куранта С=0.4. Попробуйте осуществить расчет с увеличенным временным шагом, чтобы коэффициент с был больше 1, и посмотрите, что из этого получится (такой расчет и его объяснение приведены ниже в разд. "Устойчивость").
Нелинейное уравнение
Намного более интересные решения можно получить для нелинейного уравнения теплопроводности, например, с нелинейным источником тепла ф(u)=103(u-u3). Заметим, что в листинге 11.1 мы предусмотрительно определили коэффициент диффузии и источник тепла в виде пользовательских функций, зависящих от аргумента и, т. е. от температуры. Если бы мы собирались моделировать явную зависимость их от координат, то следовало бы ввести в пользовательскую функцию в качестве аргумента переменную х, как это сделано для источника тепла ф. Поэтому нет ничего проще замены определения этих функций с констант D(U)=1 и ф(х,u)=о на новые функции, которые станут описывать другие модели диффузии тепла. Начнем с того, что поменяем четвертую строку листинга 11.1 на ф(х,и)=ю3-(и-и3), не изменяя пока постоянного значения коэффициента диффузии.
Примечание 3
Примечание 3
С физической точки зрения, зависимость коэффициента диффузии и функции источника тепла от температуры означает, что эти параметры будут меняться от точки к точке среды, определяясь локальными значениями текущей температуры в этих точках. Ввод ненулевого источника тепла означает, что среда получает определенное количество тепла, тем большее, чем больше локальная температура. Можно догадаться, что введение такой зависимости может моделировать, в частности, горение среды.
Если осуществить расчеты с упомянутым источником (имеющим кубическую нелинейность), то получится очень интересное решение уравнения теплопроводности, имеющее профиль тепловых фронтов. С течением времени граница раздела высокой и низкой температуры распространяется в обе стороны от зоны первичного нагрева, оставаясь весьма четко выделенной (Рисунок 11.8).
Еще более неожиданные решения возможны при нелинейности также и коэффициента диффузии. Например, если взять квадратичный коэффициент диффузии D(x,u)=u2 (что с учетом его умножения на неизвестные функции создаст кубическую нелинейность уравнения), а также ф(х,u)=103-u3-5, то вы сможете наблюдать совсем иной режим горения среды. В отличие от рассмотренного эффекта распространения тепловых фронтов, горение оказывается локализованным в области первичного нагрева среды, причем температура в центре нагрева со временем возрастает до бесконечной величины (Рисунок 11.9). Такое решение описывает так называемый режим горения "с обострением".
