Результат выдаваемый встроенной функцией в качестве решения системы ОДУ (продолжение листинга 9 3}
Рисунок 9.5. Результат, выдаваемый встроенной функцией в качестве решения системы ОДУ (продолжение листинга 9.3}
Первая строка листинга представляет задание параметров модели, вторая — начального условия задачи Коши, а в третьей строке листинга определено число шагов, на которых рассчитывается решение. Самая важная — это предпоследняя строка листинга, в которой, собственно, определяется система ОДУ. Последняя строка присваивает матричной переменной и результат действия функции rkfixed. Решение системы ОДУ будет осуществлено на промежутке (0,40).
Сравните рассматриваемую систему (см. разд. 9.1.Т), записанную в стандартной форме с формальной ее записью в Mathcad, чтобы не делать впоследствии ошибок. Во-первых, функция D, входящая в число параметров встроенных функций для решения ОДУ, должна быть функцией обязательно двух аргументов. Во-вторых, второй ее аргумент должен быть вектором того же размера, что и сама функция о. В-третьих, точно такой же размер должен быть и у вектора начальных значений у0. Не забывайте, что векторную функцию D(t,y) следует определять через компоненты вектора у с помощью кнопки Subscript (Нижний индекс) с наборной панели Calculator (Калькулятор) или нажатием клавиши <[>.
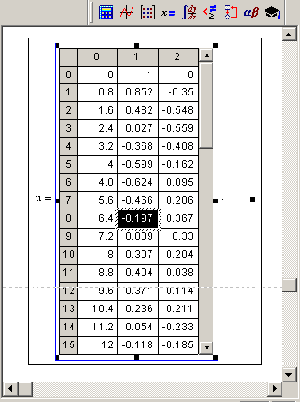
Матрица, представляющая решение, показана на Рисунок 9.5. Размер полученной матрицы будет равен (M+i)x(N+l), т. е. 51x3. Просмотреть все компоненты матрицы и, которые не помещаются на экране, можно с помощью вертикальной полосы прокрутки. Как нетрудно сообразить, на этом рисунке отмечены выделением расчетные значения искомых векторов на 10-м шаге. Это соответствует, с математической точки зрения, найденным значениям уо(8.0)=о. 307 и yi (8.0) =0.204. Для вычисления элементов решения в последней точке интервала используйте вывод элемента ин, ь Для построения графика решения надо отложить соответствующие компоненты матрицы решения по координатным осям: значения аргумента и<0> — вдоль оси х, а u<1> и u<2> — вдоль оси Y (Рисунок 9.6).
