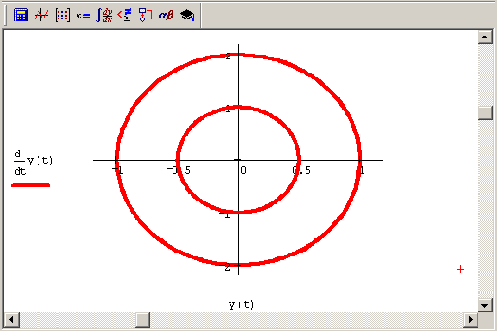
Решение уравнения со2у' '+у=0 для различных начальных условий (коллаж графиков)
Рисунок 9.3. Решение уравнения со2-у' '+у=0 для различных начальных условий (коллаж графиков)
Резюмируя содержание вводного раздела главы, перечислим еще раз типичные постановки задач, характерные для динамических систем:
- решение одной задачи Коши для ОДУ;
- исследование фазового портрета (поиск аттракторов);
- отыскание зависимости положения аттракторов в фазовом пространстве от параметров модели и фиксация бифуркационных значений параметров.
В дальнейших разделах этой главы при рассказе о возможностях Mathcad мы будем в первую очередь описывать решение первой (базовой) задачи, для которой предусмотрен целый арсенал средств. А именно: вычислительный блок для решения ОДУ (см. разд. 9.2), несколько встроенных функций для решения систем ОДУ (см. разд. 9.3), в том числе жестких, которые не поддаются решению стандартными методами (см. разд. 9.4). Приемы, которые автор рекомендует в качестве идиом решения остальных задач, будут рассмотрены эпизодически, на конкретных примерах классических динамических систем вычислительной физики, химии и биологии (см. разд. 9.5 и 9.4.3), связанных с динамическими системами. В частности, программа для визуализации фазового портрета рассмотрена в конце главы, на примере модели брюсселятора (см. разд. 9.5.4). Сводка алгоритмов с рекомендациями по их применению в зависимости от типа задачи приведена конспективно, без детального разбора (см. разд. 9.3.4).
