График решения (слева) и фазовый портрет (справа) уравнения Ван дер Поля (продолжение листинга 9 14)
Рисунок 9.19. График решения (слева) и фазовый портрет (справа) уравнения Ван дер Поля (продолжение листинга 9.14)
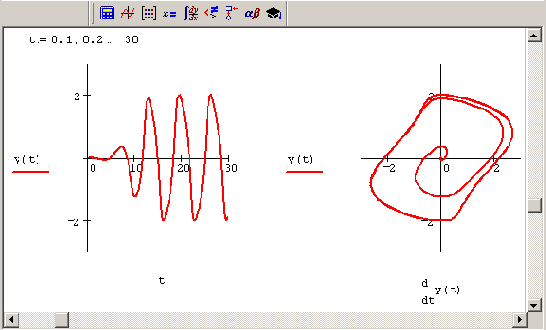
Решением уравнения Ван дер Поля являются колебания, вид которых для µ=1 показан на Рисунок 9.19. Они называются автоколебаниями и принципиально отличаются от рассмотренных нами ранее (например, колебаний маятника в модели осциллятора или численности популяций в модели Вольтерpa) тем, что их характеристики (амплитуда, частота, спектр) не зависят от начальных условий, а определяются исключительно свойствами самой динамической системы. Через некоторое время расчетов после выхода из начальной точки решение выходит на один и тот же цикл колебаний, называемый предельным циклом. Аттрактор типа предельного цикла является замкнутой кривой на фазовой плоскости. К нему асимптотически притягиваются все окрестные траектории, выходящие из различных начальных точек, как изнутри (Рисунок 9.19), так и снаружи (Рисунок 9.20) предельного цикла.
Примечание 1
Примечание 1
Если компьютер у вас не самый производительный, то расчет в Mathcad фазового портрета с Рисунок 9.19, 9.20 может занять относительно продолжительное время, что связано с численным определением сначала решения y(t), а потом его производной. Время расчетов можно было бы существенно сократить, если использовать вместо вычислительного блока Given/odesolve одну из встроенных функций, которые выдают решение в виде матрицы, например, rkfixed.
Примечание 2
Примечание 2
По мере возрастания параметра µ модель Ван дер Поля становится все более жесткой. Например, при ц=5000 решение уже придется искать при помощи специфических методов решения жестких задач (см. разд. 9.3). Это еще раз доказывает, что одна и та же система ОДУ с различными коэффициентами может быть жесткой в разной степени.
